1387. Underground cables

A city wants to get rid of their unsightly power poles by moving their power cables underground. They have a list of points that all need to be connected, but they have some limitations. Their tunneling equipment can only move in straight lines between points. They only have room for one underground cable at any location except at the given points, so no two cables can cross.

Given a list of points, what is the least amount of cable necessary to make sure that every pair of points is connected, either directly, or indirectly through other points?

Input. There are several test cases. Each test case starts with an integer n (2 ≤ n ≤ 1000), which is the number of points in the city. On each of the next n lines will be two integers x and y (-1000 ≤ x, y ≤ 1000), which are the (x, y) locations of the n points. Within a test case, all points will be distinct. The input will end with a line with a single 0.

Output. For each test case output a single real number, representing the least amount of cable the city will need to connect all of its points. Print this number with exactly two decimal places, rounded. Print each number on its own line with no spaces. Do not print any blank lines between answers.

Sample input	Sample output
4 0 0 0 10 10 0 10 10 2 0 0 10 10 0	30.00 14.14

SOLUTION

graphs – Prims algorithm

Algorithm analysis

To solve the problem, you need to find the minimum spanning tree (MST). Implement Prim algorithm.

Example

Consider two graphs, gven in a sample.

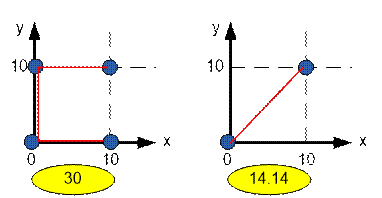
Algorithm realization

Declare the arrays. Store the point’s coordinates in (x[i], y[i]).

#define MAX 1010

int x[MAX], y[MAX];

int used[MAX], min_e[MAX], end_e[MAX];

The function dist2 computes the squared distance between cities i and j.

int dist2(int i, int j)

{

return (x[j] - x[i])*(x[j] - x[i]) + (y[j] - y[i])*(y[j] - y[i]);

}

The main part of the program. Proces several tests cases.

while (scanf("%d", &n), n)

{

Read the points coordinates.

for (i = 0; i < n; i++)

scanf("%d %d", &x[i], &y[i]);

Initialize the arrays.

memset(min_e, 0x3F, sizeof(min_e));

memset(end_e, -1, sizeof(end_e));

memset(used, 0, sizeof(used));

The size of MST will be calculated in the dist variable.

dist = min_e[1] = 0;

for (i = 0; i < n; i++)

{

Look for the vertex v with minimum value of min_e[v] among the vertices that are not yet included in MST (for which used[v] = 0).

v = -1;

for (j = 0; j < n; j++)

if (!used[j] && (v == -1 || min_e[j] < min_e[v])) v = j;

Include the vertex v into MST. Add an edge (v, end_e[v]) to MST.

used[v] = 1;

if (end_e[v] != -1) dist += sqrt((double)dist2(v, end_e[v]));

Recompute the labels for the edges outgoing from v.

Iterate over only those vertices to that are not yet included in MST (used [to] = 0).

for (to = 0; to < n; to++)

{

int dV_TO = dist2(v, to);

if (!used[to] && (dV_TO < min_e[to]))

{

min_e[to] = dV_TO;

end_e[to] = v;

}

}

}

Print the value of MST.

printf("%.2lf\n", dist);

}